Dissipative Ising Model
In this tutorial, we will use exact diagonalization, VMPOMC.jl and t-VMPOMC.jl to study the properties of a class of dissipative transverse-field Ising models.
Recommended tutorials
Introduction
We consider a transverse-field Ising model in one-dimension described by the Hamiltonian \begin{equation} H = J\sum_i \sigma^z_i \sigma^z_{i+1} + h\sum_i \sigma^x_i. \end{equation} The ground state properties of the system are well understood. Here, we are interested in exploring its non-equilibrium properties. We assume that the interactions of the system of spins with the external enviornment is well described by a Markovian Lindblad master equation for the many-body density matrix $\rho$, \begin{equation} \partial_t \rho = -i[H,\rho] + \sum_k \left(\Gamma_k \rho \Gamma_k^\dagger - \frac{1}{2}{\Gamma_k^\dagger \Gamma_k,\rho}\right) := \mathcal{L}[\rho] \end{equation} The superoperator $\mathcal{L}$ is often referred to as the Lindbladian. Here, each jump operator $\Gamma_k$ encodes a specific dissipative process acting on site $k$. In this example we choose \begin{equation} \Gamma_k = \sqrt{\gamma}\,\sigma^-_k, \end{equation} where
- $\sigma^- = (\sigma^x - i\sigma^y)/2$ is the spin-lowering operator on a single site.
- $\gamma$ is the dissipation rate (we set $\gamma=1$ in our units).
Physically, $\Gamma_k$ implements spontaneous emission of an excited spin into the environment, driving each spin toward the $|\downarrow\rangle$ state. The competition among the interaction between neighbouring spins ($J\sigma^z_i\sigma^z_{i+1}$), coherent transverse-field flips ($h\sigma^x$) and dissipative decay ($\sqrt{\gamma}\sigma^-$) gives rise to nontrivial non-equilibrium dynamics and steady states. Other common choices include:
- Dephasing: $\Gamma_k = \sqrt{\gamma_z}\sigma^z_k$, which randomizes the relative phase in the $[\ket{\uparrow}, \ket{\downarrow}]$ basis without changing populations.
- Collective decay: $\Gamma = \sqrt{\gamma_c},\sum_k \sigma^-_k$, coupling the entire chain to a common bath and leading to superradiant effects.
Steady state
We will begin by investigating the non-equilibrium steady state of the model, i.e. the fixed point of the dynamics reached at very long times, $\partial_t \rho = 0$. We will do so with the help of exact diagonalization and the time-independent variational principle.
Exact diagonalization
Let us begin by constructing and diagonalizing the Lindbladian superoperator. We first load the necessary packages and define Pauli operators, along with their sparse variants:
using LinearAlgebra, SparseArrays, ArnoldiMethod
⊗(x,y) = kron(x,y)
id = [1.0+0.0im 0.0+0.0im; 0.0+0.0im 1.0+0.0im]
sx = [0.0+0.0im 1.0+0.0im; 1.0+0.0im 0.0+0.0im]
sy = [0.0+0.0im 0.0-1im; 0.0+1im 0.0+0.0im]
sz = [1.0+0.0im 0.0+0.0im; 0.0+0.0im -1.0+0.0im]
sp = (sx+1im*sy)/2
sm = (sx-1im*sy)/2
sp_id = sparse(id)
sp_sx = sparse(sx)
sp_sy = sparse(sy)
sp_sz = sparse(sz)
sp_sp = sparse(sp)
sp_sm = sparse(sm)
We then construct the Ising Hamiltonian:
function one_body_Hamiltonian_term(N::Int64, op::SparseMatrixCSC{ComplexF64, Int64})
ops = fill(sp_id, N)
ops[1] = op
H = spzeros(ComplexF64, 2^N, 2^N)
for _ in 1:N
H += foldl(⊗, ops)
ops = circshift(ops,1)
end
return H
end
function two_body_Hamiltonian_term(N::Int64, op::SparseMatrixCSC{ComplexF64, Int64})
ops = fill(sp_id, N)
ops[1] = op
ops[2] = op
H = spzeros(ComplexF64, 2^N, 2^N)
for _ in 1:N
H += foldl(⊗, ops)
ops = circshift(ops,1)
end
return H
end
N = 8
J = 0.5
h = 1.0
H = J * two_body_Hamiltonian_term(N, sp_sz) + h * one_body_Hamiltonian_term(N, sp_sx)
The Lindbladian can be expressed as a matrix in Liouville space. The (non-unique) isomorphism is given by \begin{align} \mathcal{L} &= -i( H\otimes \mathbb{1} - \mathbb{1} \otimes H^\top ) + \sum_k \left(\Gamma_k \otimes \Gamma_k^* - \frac{1}{2}\Gamma_k^\dagger \Gamma_k \otimes \mathbb{1} - \frac{1}{2} \mathbb{1} \otimes \Gamma_k^\top \Gamma_k^* \right). \end{align} In Julia:
function one_body_Lindbladian_term(N::Int64, op::SparseMatrixCSC{ComplexF64, Int64})
ops = fill(sp_id, N)
ops[1] = op
Id = foldl(⊗, fill(sp_id, N))
L_D = spzeros(ComplexF64, 2^(2*N), 2^(2*N))
for _ in 1:N
Γ = foldl(⊗, ops)
ops = circshift(ops,1)
L_D += Γ⊗conj(Γ) - (conj(transpose(Γ))*Γ)⊗Id/2 - Id⊗(transpose(Γ)*conj(Γ))/2
end
return L_D
end
γ = 1.0
Id = foldl(⊗, fill(sp_id, N))
L = -1im*(H⊗Id - Id⊗transpose(H)) + γ * one_body_Lindbladian_term(N, sp_sm)
L is now a sparse, non-Hermitian, square matrix, which can be diagonalized via the Arnoldi method. We write:
function eigen_sparse(x, n)
decomp, history = partialschur(x, nev=n, which=:LR, restarts=100000);
vals, vecs = partialeigen(decomp);
return vals, vecs
end
evals, evecs = eigen_sparse(L, 6)
display(evals)
This finds the 6 largest eigenvalues, which are found to be all non-positive, with one zero eigenvalue associated with the unique steady state:
6-element Vector{ComplexF64}:
-1.0265353581717023 - 3.36845317347161e-11im
-1.0258847238574662 - 4.232719954352772e-10im
-1.0174169414337269 + 2.594555839820057im
-1.017416941284772 - 2.594555839810845im
-0.5105598311206574 + 4.4948856307595167e-10im
-3.1922988069600096e-10 + 9.084818965830727e-11im
The eigenvector associated with the zero eigenvalues can be reshaped and renormalized to obtain the steady-state density matrix:
ρ = reshape(evecs[:,end] ,2^N, 2^N)
ρ./=tr(ρ)
display(ρ)
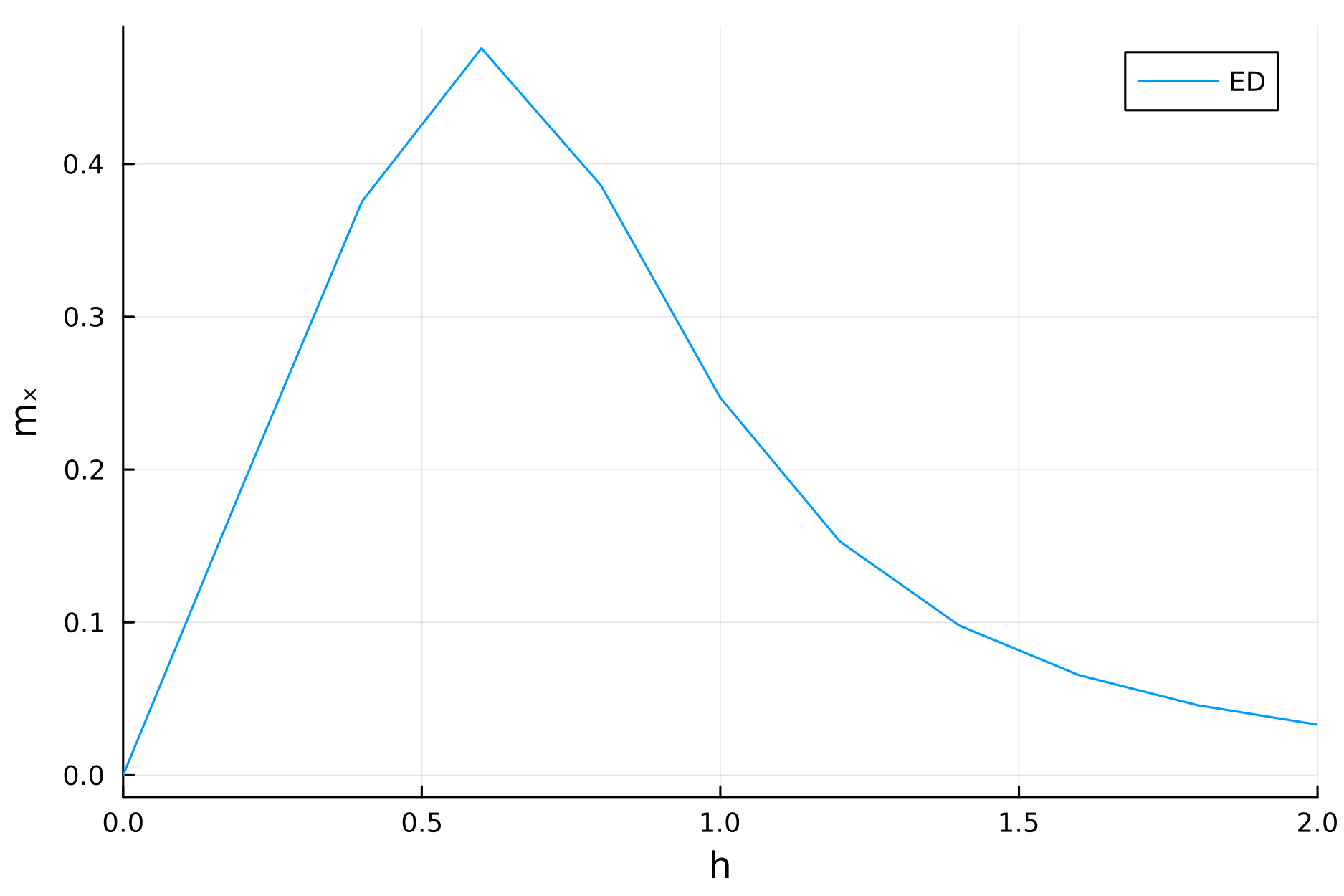
One can then, for example, study the steady-state magnetization phase diagram as function of the transverse field strength $h$, given by $m_x = \text{tr}\, {\sigma^x\rho}$. This can be achieved via
function magnetization(op, site::Int64, ρ::Matrix{ComplexF64}, N::Int64)
first_term_ops = fill(id, N)
first_term_ops[site] = op
m = tr(ρ*foldl(⊗, first_term_ops))
return m
end
mx_list = []
h_range = 0.0:0.2:2.0
for h=h_range
H = J * two_body_Hamiltonian_term(N, sp_sz) + h * one_body_Hamiltonian_term(N, sp_sx)
L = -1im*(H⊗Id - Id⊗transpose(H)) + γ * one_body_Lindbladian_term(N, sp_sm)
evals, evecs = eigen_sparse(L, 2)
ρ = reshape(evecs[:,end],2^N,2^N)
ρ./=tr(ρ)
mx = magnetization(sx, 1, ρ, N)
push!(mx_list, real(mx))
end
using Plots
plot(h_range, mx_list, xlims=(0,2), xlabel="h", ylabel="mₓ")
This produces the below figure:
VMPOMC
Exact diagonalization of the Liouvillian scales exponentially in system size and quickly becomes intractable. To reach $N=20$ spins, we employ the variational matrix product operator Monte Carlo (VMPOMC) method, which approximates the steady-state density operator $\rho_{ss}$ as a parameterized MPO and optimizes it stochastically. Below is a minimal script:
include("VMPOMC.jl")
using .VMPOMC
using LinearAlgebra
using MPI
MPI.Init()
mpi_cache = set_mpi()
N = parse(Int64, ARGS[1])
h = parse(Float64, ARGS[2])
χ = parse(Int64, ARGS[3])
# Physical parameters
const J = 0.5
const γ = 1.0
# Optimization hyperparameters
const N_MC = 250
const δ = 0.1
const F = 0.998
const ϵ = 0.1
const N_iterations = 5000
const cost_function_threshold = 1e-4
# Initialize parameters (use positional arguments)
params = Parameters(N=N, χ=χ, J=J, hx=h, γ=γ)
# Define the one-body Lindbladian:
l1 = make_one_body_Lindbladian(h*sx, sqrt(γ)*sm)
# Initialize MPO on all processes
A = Array{ComplexF64}(undef, χ, χ, 4)
if mpi_cache.rank == 0
A_init = rand(ComplexF64, χ, χ, 2, 2)
A = reshape(A_init, χ, χ, 4)
end
MPI.Bcast!(A, 0, mpi_cache.comm)
# Define sampler and optimizer
sampler = MetropolisSampler(N_MC, 2)
optimizer = Optimizer("SR", sampler, A, l1, ϵ, params, "Ising", "Local")
# Variable to track convergence
converged = false
for k in 1:N_iterations
# Optimize MPO
compute_gradient!(optimizer)
MPI_mean!(optimizer, mpi_cache)
if mpi_cache.rank == 0
optimize!(optimizer, δ*F^k)
end
MPI.Bcast!(optimizer.A, 0, mpi_cache.comm)
if mpi_cache.rank == 0
# Calculate energy per site
cost_function = real(optimizer.optimizer_cache.mlL)/N
# Check for convergence (cost_function below threshold)
if abs(cost_function) < cost_function_threshold
global converged = true
end
# Print progress every 100 iterations or on final iteration
if mod(k, 100) == 0 || converged
# Calculate steady-state magnetizations
mx = tensor_calculate_magnetization(optimizer, sx)
println("Iteration $k:")
println(" Cost Function: $(round(cost_function, digits=6))")
println(" Magnetization: mx=$(round(mx, digits=4))")
end
end
# Broadcast convergence status to all processes
MPI.bcast(converged, mpi_cache.comm)
# Exit loop if converged
if converged
break
end
end
if mpi_cache.rank == 0
if converged
# Record magnetization
mx = tensor_calculate_magnetization(optimizer, sx)
o = open("Ising_h=$(h)_mx.txt", "a")
println(o, real(mx))
close(o)
println("Optimization completed successfully with convergence!")
else
println("Optimization completed - maximum iterations reached without convergence.")
energy = real(optimizer.optimizer_cache.mlL)/N
println("Final Cost Function: $(round(energy, digits=8))")
end
end
MPI.Finalize()
exit(0)
This script can be ran by executing
mpirun -np X julia vmpomc_ising.jl N h chi
where X specifies the number of MPI processes, N is the number of sites, h is the local field strength, and chi is the bond dimension.
Note on hyperparameters:
The above script makes use of five hyperparameters that control the gradient descent optimization:
N_MC: Number of Monte Carlo samples used in the Metropolis sampler. Increasing this improves sampling accuracy but increases computational cost.δ: Initial learning rate scaling factor for the optimizer.F: Learning rate decay factor per iteration, controlling how the learning rate decreases over time.ϵ: Regularization parameter used in the optimizer to stabilize the inversion of the metric matrix. Effectively tunes between SGD and SR.N_iterations: Maximum number of optimization iterations.cost_function_threshold: Threshold for the cost function below which optimization is considered converged. Ideally, we want this to be as close to 0 as possible.Adjusting these parameters affects convergence speed and stability. Start with the above pre-set defaults and tune based on problem size, bond dimension, and observed convergence behavior.
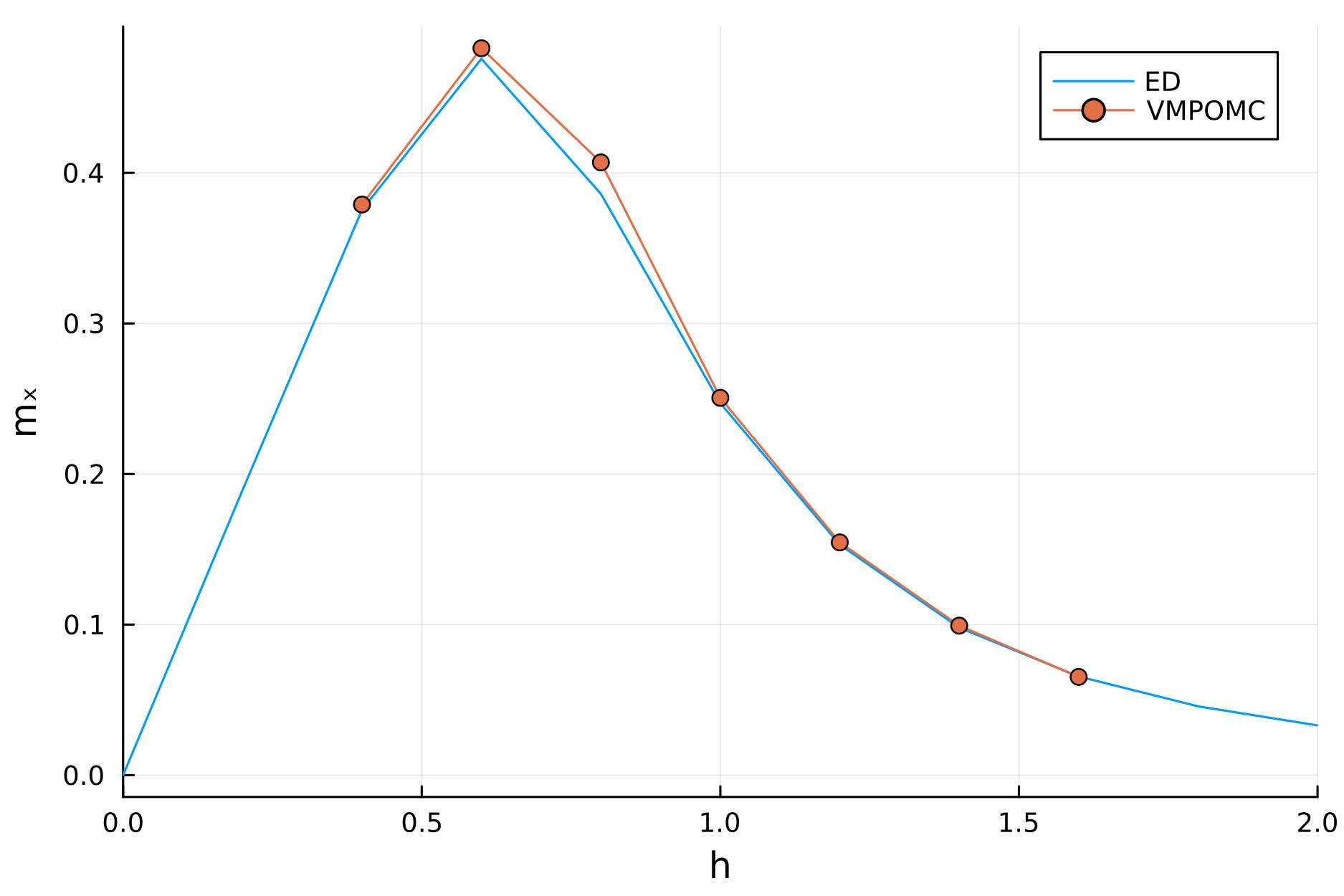
To reproduce the phase diagram as in ED, we can run the bash script:
#!/bin/bash
N=20
CHI=6
for i in $(seq 2 8); do
h=$(echo "scale=1; $i / 5.0" | bc)
echo "Running h = $h"
mpirun -np 4 julia vmpomc_ising.jl $N $h $CHI
done
echo "Done"
The converged magnetizations for $N=20$ can now be loaded and plotted against ED results for $N=8$, showing excellent agreement:
Exercises
- A bond dimension of $χ=6$ is found to give accurate estimates of the magnetization at low computational overhead at $N=20$, but larger χ improves fidelity at increased cost. To see this, fix the value of the local field $h$ and plot the converged magnetizations as function of the bond dimension, starting from $χ=1$, tracking the attained values of the cost function. Use the
time()function in Julia to also track the total optimization time. Observe how an insufficiently small bond dimension causes the cost function to plateau at a value that may higher than the set threshold, preventing the results from ever converging.- What happens when we increase or decrease the interaction strength $J$? What is the minimum bond dimension required for convergence in those cases?
- Try to vary and find the optimal hyperparameter values that lead to most rapid convergence. How much can the convergence threshold be loosened before the results become inaccurate?
- Suppose the interaction with the external environment leads to spin decay to the $\ket{\rightarrow}$ state, described by the Lindblad jump operator $\Gamma_k = \sqrt{\gamma}(\sigma^z - i\sigma^y)/2$. Compare the resultant phase diagrams for $m_x$, $m_y$, and $m_z$.
- Instead of starting each optimization process from a completely random MPO, it may be more efficient to load an already converged MPO at slightly different model parameter values. Try implementing this by appropriately modifying the above scripts.
Dynamics
To be completed.
Two-dimensional lattices - iPEPO
To be completed.